Closest-Packing or Gravitational Gathering of Spheres

by Bill Lauritzen

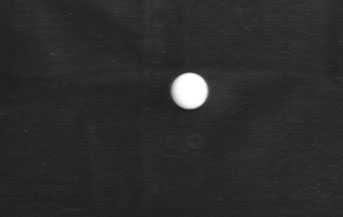
one sphere

two spheres

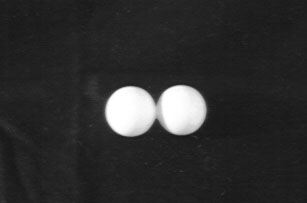
two spheres gravitationally packed

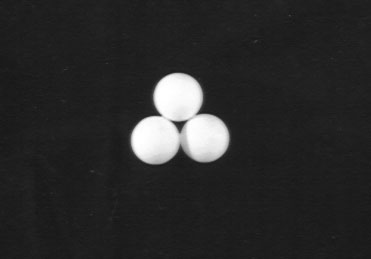
3 spheres closest-packed

4 spheres closest-packed (tetrahedron or 4-nook)

5 spheres

6 spheres (octahedron or 6-nook)

7 spheres

8 (closest-packed and 90-degree packed). Which is more stable?

9 spheres

10 spheres (two packing methods)

11 spheres

12 (icosahedron or 12-nook)

13 (12 around 1) nucleated

19 and 19 (in octahedron 6-nook) (14 in a pyramid)

35 in tetrahedral (4-nook pattern)

35 (side view)

42 around 12 around 1 = 55 nucleated

number of spheres in the outer layer = 10F^2 + 2, where F is the frequency or number of layers

octahedral shape

7 (6 around 1 in a plane)

19= 12 around 6 around 1 in a plane

60 degree versus 90 degree packing. Which packs closer? Which is more stable?

60 degree versus 90 degree packing. Which packs closer? Which is more stable?

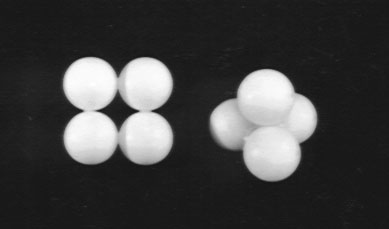
60 degree versus 90 degree packing in space. Which packs closer? Which is more stable?

60 degree versus 90 degree packing. Which packs closer? Which is more stable?

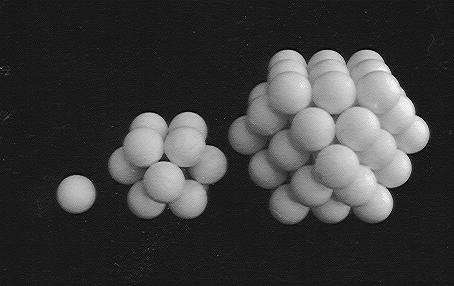
1 surrounded by 12 surround by 42 pattern

left: 1 frequency octahedron, right: 2 frequency octahedron, middle: 19 (shown before)

1 and 2 frequency octahedra (12-nooks)

1, 2, 3, 4, 6, and 12 spheres make regular (all-even) shapes.

spheres corresponding to tetrahedron, octahedron, and icosahedron. (4-nook, 6-nook, and 12-nook)

Key words: geometry, art, science, mathematics, design, packing, economics, space, architecture, polyhedron, polyhedra.